Capítulo 4 Regressão Linear
A essência de uma regressão linear é ajustarmos um modelo aos nossos dados e o usarmos ele para prever valores da variável dependente (VD) a partir de uma ou mais variáveis independentes (VIs). A análise de regressão é uma maneira de prever uma variável de resultado a partir de uma variável preditora (regressão simples) ou várias variáveis preditoras (regressão múltipla) (Field, Miles, and Field 2012).
Na regressão linear, a variável que estaríamos tentando descobrir, variável dependente, é o “y” da função. E as variáveis que exercem influência sobre a dependente, variáveis independentes, são os “Xs” da função. O modelo que ajustamos por meio dessa função é linear, o que significa que resumimos um conjunto de dados com uma linha reta (no caso de regressão simples) ou um plano (no caso de regressão múltipla). Para isso, usamos uma técnica matemática chamada método dos mínimos quadrados para estabelecer a reta ou plano que melhor descreve os dados coletados, conforme a figura representada abaixo (Field, Miles, and Field 2012):
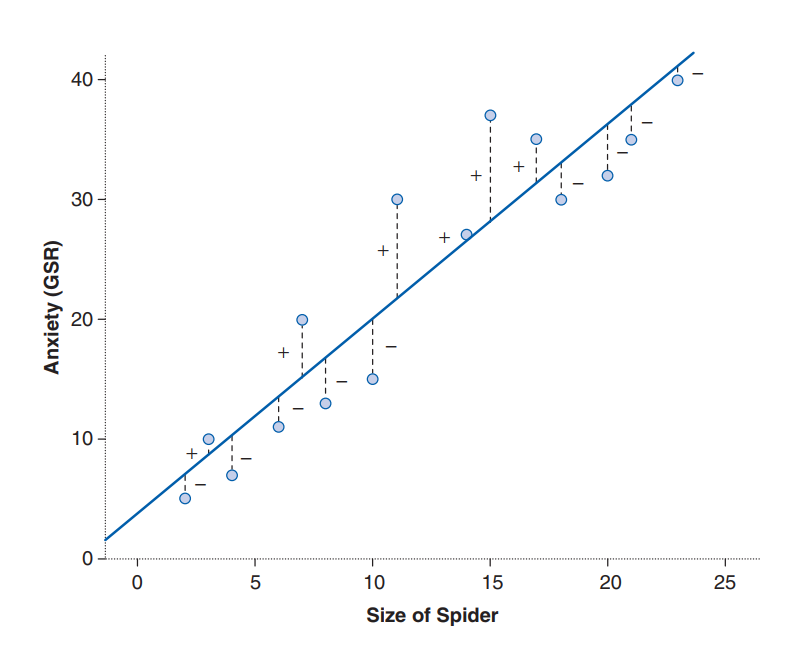
Essa linha ou plano pode ser definida por dois coisas: (1) a inclinação (ou gradiente) da linha ou plano (geralmente denotada por \(\beta_{1}\), \(\beta_{2}\), …, \(\beta_{n}\)), relacionado a cada variável independente respectivamente (\(X_{1}\), \(X_{2}\), …, \(X_{n}\)); e (2) o ponto em qual a linha cruza o eixo y do gráfico (conhecido como intercepto \(\beta_{0}\)). Dessa forma temos a equação de regressão abaixo, na qual \(y_{i}\) é o resultado que queremos prever e \(X_{1i}\), \(X_{2i}\), …, \(X_{ni}\) são os valores da \(i\)-ésima instância de cada na variável preditora. \(\beta_{0}\), \(\beta_{1}\), \(\beta_{2}\), …, \(\beta_{n}\) são os coeficientes da regressão. Por fim, existe um termo residual, \(\epsilon_{i}\), que representa a diferença entre o valor prevista pela linha ou plano para uma instância \(i\) qualquer e o valor que real para essa respectiva instância. Podemos muitas vezes ver a equação representada sem esse termo residual, mas é importante atentarmos para sua existência, pois ele evidencia que o modelo não se ajustará perfeitamente aos dados:
\(y_{i} = \beta_{0} + \beta_{1}X_{1i} + \beta_{2}X_{2i} + \beta_{3}X_{3i} + ... + \beta_{n}X_{ni} + \epsilon_{i}\)
O código a seguir pode ser utilizado para estimar um modelo de regressão linear no software R. Vamos utilizar a base de dados Album Sales 2.dat disponibilizada por (Field, Miles, and Field 2012) no repositório digital de seu livro. Para fins da aplicação da regressão linear, vamos assumir que essa base dados refere-se aos dados de 200 álbuns de música. A base possui quatro colunas, (\(i\)) sales: representando a quantidade cada álbum que é vendida; (\(ii\)) adverts: representando os valores gastos com propaganda para cada álbum; (\(iii\)) airplay: representando a quantidade de vezes que o álbum foi tocado nas rádios; (\(iv\)) attract: a atratividade da banda.
# Carregar base de dados Album Sales 2.dat do livro de Field et al. (2012)
albumSales <- read.delim(
# No parâmetro file, use o caminho para a pasta onde está
# o arquivo Album Sales 2.dat em seu computador.
file = "dados/Album Sales 2.dat",
header = TRUE
)
albumSales## adverts sales airplay attract
## 1 10.256 330 43 10
## 2 985.685 120 28 7
## 3 1445.563 360 35 7
## 4 1188.193 270 33 7
## 5 574.513 220 44 5
## 6 568.954 170 19 5
## 7 471.814 70 20 1
## 8 537.352 210 22 9
## 9 514.068 200 21 7
## 10 174.093 300 40 7
## 11 1720.806 290 32 7
## 12 611.479 70 20 2
## 13 251.192 150 24 8
## 14 97.972 190 38 6
## 15 406.814 240 24 7
## 16 265.398 100 25 5
## 17 1323.287 250 35 5
## 18 196.650 210 36 8
## 19 1326.598 280 27 8
## 20 1380.689 230 33 8
## 21 792.345 210 33 7
## 22 957.167 230 28 6
## 23 1789.659 320 30 9
## 24 656.137 210 34 7
## 25 613.697 230 49 7
## 26 313.362 250 40 8
## 27 336.510 60 20 4
## 28 1544.899 330 42 7
## 29 68.954 150 35 8
## 30 785.692 150 8 6
## 31 125.628 180 49 7
## 32 377.925 80 19 8
## 33 217.994 180 42 6
## 34 759.862 130 6 7
## 35 1163.444 320 36 6
## 36 842.957 280 32 7
## 37 125.179 200 28 6
## 38 236.598 130 25 8
## 39 669.811 190 34 8
## 40 612.234 150 21 6
## 41 922.019 230 34 7
## 42 50.000 310 63 7
## 43 2000.000 340 31 7
## 44 1054.027 240 25 7
## 45 385.045 180 42 7
## 46 1507.972 220 37 7
## 47 102.568 40 25 8
## 48 204.568 190 26 7
## 49 1170.918 290 39 7
## 50 689.547 340 46 7
## 51 784.220 250 36 6
## 52 405.913 190 12 4
## 53 179.778 120 2 8
## 54 607.258 230 29 8
## 55 1542.329 190 33 8
## 56 1112.470 210 28 7
## 57 856.985 170 10 6
## 58 836.331 310 38 7
## 59 236.908 90 19 4
## 60 1077.855 140 13 6
## 61 579.321 300 30 7
## 62 1500.000 340 38 8
## 63 731.364 170 22 8
## 64 25.689 100 23 6
## 65 391.749 200 22 9
## 66 233.999 80 20 7
## 67 275.700 100 18 6
## 68 56.895 70 37 7
## 69 255.117 50 16 8
## 70 566.501 240 32 8
## 71 102.568 160 26 5
## 72 250.568 290 53 9
## 73 68.594 140 28 7
## 74 642.786 210 32 7
## 75 1500.000 300 24 7
## 76 102.563 230 37 6
## 77 756.984 280 30 8
## 78 51.229 160 19 7
## 79 644.151 200 47 6
## 80 15.313 110 22 5
## 81 243.237 110 10 8
## 82 256.894 70 1 4
## 83 22.464 100 1 6
## 84 45.689 190 39 6
## 85 724.938 70 8 5
## 86 1126.461 360 38 7
## 87 1985.119 360 35 5
## 88 1837.516 300 40 5
## 89 135.986 120 22 7
## 90 237.703 150 27 8
## 91 976.641 220 31 6
## 92 1452.689 280 19 7
## 93 1600.000 300 24 9
## 94 268.598 140 1 7
## 95 900.889 290 38 8
## 96 982.063 180 26 6
## 97 201.356 140 11 6
## 98 746.024 210 34 6
## 99 1132.877 250 55 7
## 100 1000.000 250 5 7
## 101 75.896 120 34 6
## 102 1351.254 290 37 9
## 103 202.705 60 13 8
## 104 365.985 140 23 6
## 105 305.268 290 54 6
## 106 263.268 160 18 7
## 107 513.694 100 2 7
## 108 152.609 160 11 6
## 109 35.987 150 30 8
## 110 102.568 140 22 7
## 111 215.368 230 36 6
## 112 426.784 230 37 8
## 113 507.772 30 9 3
## 114 233.291 80 2 7
## 115 1035.433 190 12 8
## 116 102.642 90 5 9
## 117 526.142 120 14 7
## 118 624.538 150 20 5
## 119 912.349 230 57 6
## 120 215.994 150 19 8
## 121 561.963 210 35 7
## 122 474.760 180 22 5
## 123 231.523 140 16 7
## 124 678.596 360 53 7
## 125 70.922 10 4 6
## 126 1567.548 240 29 6
## 127 263.598 270 43 7
## 128 1423.568 290 26 7
## 129 715.678 220 28 7
## 130 777.237 230 37 8
## 131 509.430 220 32 5
## 132 964.110 240 34 7
## 133 583.627 260 30 7
## 134 923.373 170 15 7
## 135 344.392 130 23 7
## 136 1095.578 270 31 8
## 137 100.025 140 21 5
## 138 30.425 60 28 1
## 139 1080.342 210 18 7
## 140 799.899 210 28 7
## 141 1071.752 240 37 8
## 142 893.355 210 26 6
## 143 283.161 200 30 8
## 144 917.017 140 10 7
## 145 234.568 90 21 7
## 146 456.897 120 18 9
## 147 206.973 100 14 7
## 148 1294.099 360 38 7
## 149 826.859 180 36 6
## 150 564.158 150 32 7
## 151 192.607 110 9 5
## 152 10.652 90 39 5
## 153 45.689 160 24 7
## 154 42.568 230 45 7
## 155 20.456 40 13 8
## 156 635.192 60 17 6
## 157 1002.273 230 32 7
## 158 1177.047 230 23 6
## 159 507.638 120 0 6
## 160 215.689 150 35 5
## 161 526.480 120 26 6
## 162 26.895 60 19 6
## 163 883.877 280 26 7
## 164 9.104 120 53 8
## 165 103.568 230 29 8
## 166 169.583 230 28 7
## 167 429.504 40 17 6
## 168 223.639 140 26 8
## 169 145.585 360 42 8
## 170 985.968 210 17 6
## 171 500.922 260 36 8
## 172 226.652 250 45 7
## 173 1051.168 200 20 7
## 174 68.093 150 15 7
## 175 1547.159 250 28 8
## 176 393.774 100 27 6
## 177 804.282 260 17 8
## 178 801.577 210 32 8
## 179 450.562 290 46 9
## 180 26.598 220 47 8
## 181 179.061 70 19 1
## 182 345.687 110 22 8
## 183 295.840 250 55 9
## 184 2271.860 320 31 5
## 185 1134.575 300 39 8
## 186 601.434 180 21 6
## 187 45.298 180 36 6
## 188 759.518 200 21 7
## 189 832.869 320 44 7
## 190 56.894 140 27 7
## 191 709.399 100 16 6
## 192 56.895 120 33 6
## 193 767.134 230 33 8
## 194 503.172 150 21 7
## 195 700.929 250 35 9
## 196 910.851 190 26 7
## 197 888.569 240 14 6
## 198 800.615 250 34 6
## 199 1500.000 230 11 8
## 200 785.694 110 20 94.1 Regressão linear simples
Por meio da análise de regressão linear, podemos inicialmente estimar um modelo de regressão linear simples no qual a variável dependente são as quantidades vendidas dos álbuns e a variável independente é o gasto em propaganda.
# Estimar modelo de regressão linear simples
advertSalesModel <- lm(
formula = sales ~ adverts,
data = albumSales
)
summary(advertSalesModel)##
## Call:
## lm(formula = sales ~ adverts, data = albumSales)
##
## Residuals:
## Min 1Q Median 3Q Max
## -152.949 -43.796 -0.393 37.040 211.866
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.341e+02 7.537e+00 17.799 <2e-16 ***
## adverts 9.612e-02 9.632e-03 9.979 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 65.99 on 198 degrees of freedom
## Multiple R-squared: 0.3346, Adjusted R-squared: 0.3313
## F-statistic: 99.59 on 1 and 198 DF, p-value: < 2.2e-16Os resultados do modelo de regressão permitem que possamos avaliar primeiramente o ajuste do modelo aos dados por meio da análise do R-squared. O resultado para essa medida foi 0,3346. O R-squared nos indica o percentual de variação da variável sales (quantidades vendidas dos álbuns) que é explicada pela variabilidade da variável adverts (propaganda de cada álbum). Nesse caso, concluímos que 33,46% da variação nas quantidades vendidas pode ser explicada pela variação dos gastos com propaganda.
O resultado para F-statistic, refere-se à estatística F da ANOVA. A estatística F e seu respectivo valor p fornecem informações sobre a qualidade da predição feita pelo modelo. Quando o valor p-value < 0,05, podemos concluir que o modelo de regressão resulta em uma previsão significativamente melhor para quantidades vendidas dos álbuns do que se usássemos apenas o valor médio das quantidades vendidas como medida de predição. Em suma, o modelo de regressão em geral prevê as quantidades vendidas significativamente bem.
Uma vez que validamos que o modelo é razoavelmente útil, avaliamos também os coeficientes da regressão (\(\beta_{0}\) e \(\beta_{1}\)):
\(\beta_{0}\): Ao avaliarmos o valor p-value para a estatística t referente ao intercepto da regressão, observamos que p-value < 0,05, indicando que o intercepto deve fazer parte do modelo final de regressão. Além disso, o valor do intercepto (\(\beta_{0}\)) é 134,1. Isso indica que, quando nenhum gasto com propaganda é realizado (adverts = 0), o modelo prevê que a quantidade vendida seria 134,1.
\(\beta_{1}\): Ao avaliarmos o valor p-value para a estatística t referente ao \(\beta_{1}\) da regressão (coeficiente relacionado à variável independente “adverts”), observamos que p-value < 0,05, indicanddo que o \(\beta_{1}\) deve fazer parte do modelo final de regressão. Além disso, o valor de \(\beta_{1}\) é 0,096. Isso indica que, para cada aumento de 1 unidade nos gastos em propagando, espera-se que ocorra um aumento de 0,096 unidades vendidas. Por exemplo, se $1000 for gasto a mais em propaganda para determinado álbum, espera-se uma elevação de 96 unidades vendidas desse álbum.
O código abaixo pode ser utilizado para representar graficamente a reta estimada pelo modelo de regressão simples ajustado:
# Representar graficamente a reta ajustada pelo modelo de regressão linear
# simples
plot(
x = albumSales$adverts,
y = albumSales$sales,
main = "Unidades de álbuns vendidas versus propaganda",
xlab = "Valor gasto com propaganda",
ylab = "Unidades vendidas"
)
abline(advertSalesModel)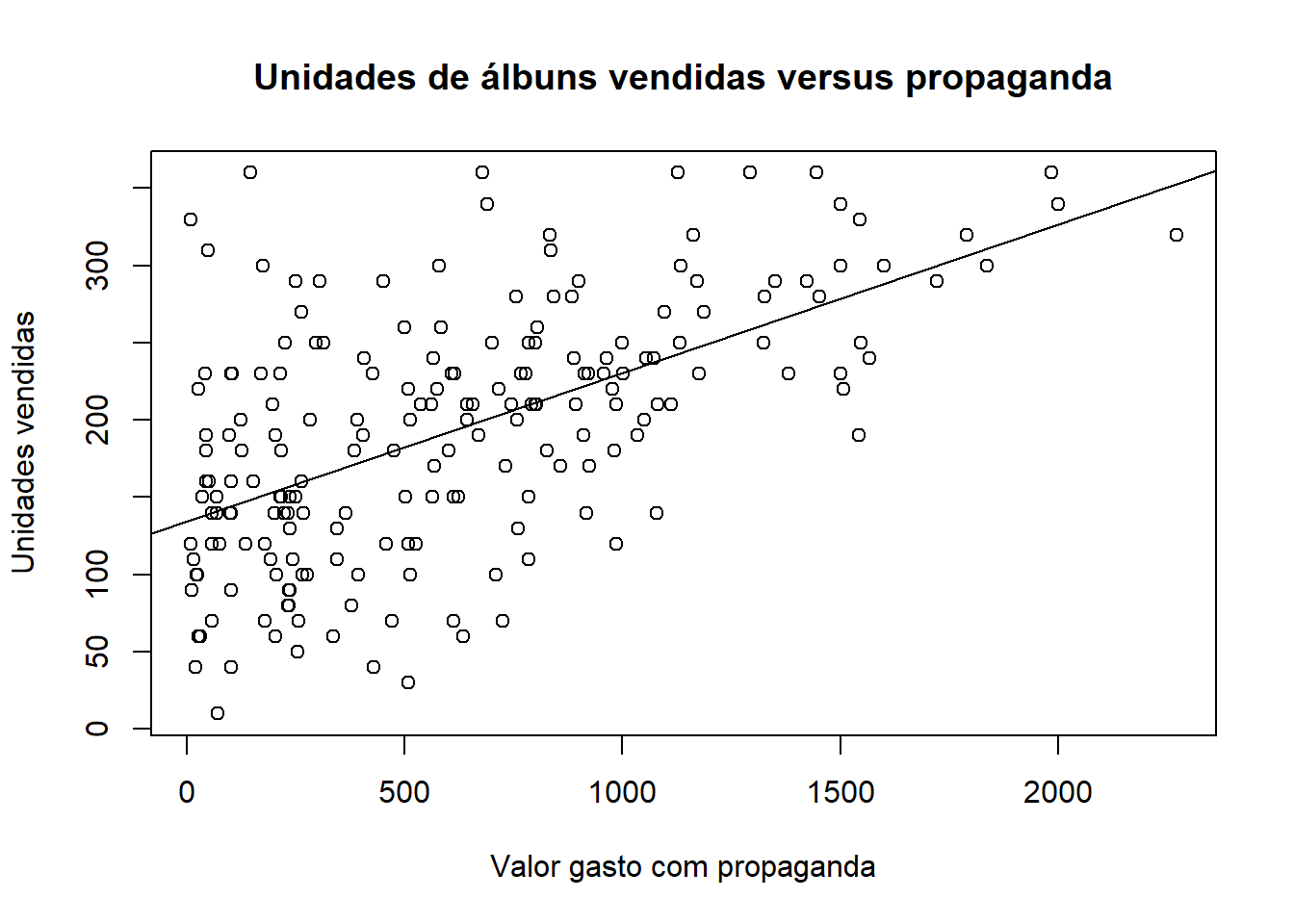
4.2 Regressão linear múltipla
Como o modelo acima é uma regressão simples, a única variável utilizada explica apenas 33,46% da variação nas quantidades vendidas. Para elevar essa performance do modelo, uma alternativa é adicionar outras variáveis independentes que possam agregar poder de explicação da quantidade vendida de álbuns.
Usando o código abaixo, podemos estimar modelo de regressão múltipla com os gastos com propaganda (adverts) e a quantidade de vezes que o álbum foi tocado nas rádios (airplay) como variáveis independentes.
# Estimar modelo de regressão linear múltipla
advertAirplaySalesModel <- lm(
formula = sales ~ adverts + airplay,
data = albumSales
)
summary(advertAirplaySalesModel)##
## Call:
## lm(formula = sales ~ adverts + airplay, data = albumSales)
##
## Residuals:
## Min 1Q Median 3Q Max
## -112.121 -30.027 3.952 32.072 155.498
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 41.123811 9.330952 4.407 1.72e-05 ***
## adverts 0.086887 0.007246 11.991 < 2e-16 ***
## airplay 3.588789 0.286807 12.513 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 49.38 on 197 degrees of freedom
## Multiple R-squared: 0.6293, Adjusted R-squared: 0.6255
## F-statistic: 167.2 on 2 and 197 DF, p-value: < 2.2e-16O resultado do R-squared evidencia como adição da variável airplay melhorou a capacidade de o modelo explicar a variabilidade da quantidade de álbuns vendidas. O resultado para essa medida foi agora 0,6255. Ou seja, concluímos que 62,55% da variação nas quantidades vendidas pode ser explicada pela variação nos gastos com propaganda e na quantidade de vezes que o álbum é tocado nas rádios.
O resultado para F-statistic (F = 167.2) e seu respectivo valor p (p-value < 0,05) indicam que o modelo de regressão resulta em uma previsão significativamente melhor para quantidades vendidas dos álbuns do que se usássemos apenas o valor médio das quantidades vendidas como medida de predição. Em suma, o modelo de regressão em geral prevê as quantidades vendidas significativamente bem.
Em relação aos coeficientes da regressão (\(\beta_{0}\), \(\beta_{1}\) e \(\beta_{2}\)), temos a seguinte avaliação:
\(\beta_{0}\): Ao avaliarmos o valor p-value para a estatística t referente ao intercepto da regressão, observamos que p-value < 0,05, indicando que o intercepto deve fazer parte do modelo final de regressão. Além disso, o valor do intercepto (\(\beta_{0}\)) é 41,12. Isso indica que, quando nenhum gasto com propaganda é realizado (adverts = 0) e quando o álbum não é tocado nenhuma vez nas rádios (airplay = 0), o modelo prevê que a quantidade vendida seria 41,12.
\(\beta_{1}\): Ao avaliarmos o valor p-value para a estatística t referente ao \(\beta_{1}\) da regressão (coeficiente relacionado à variável independente “adverts”), observamos que p-value < 0,05, indicanddo que o \(\beta_{1}\) deve fazer parte do modelo final de regressão. Além disso, o valor de \(\beta_{1}\) é 0,087. Isso indica que, para cada aumento de 1 unidade nos gastos em propagando, espera-se que ocorra um aumento de 0,087 unidades vendidas. Por exemplo, se $1000 for gasto a mais em propaganda para determinado álbum, espera-se uma elevação de 87 unidades vendidas desse álbum.
\(\beta_{2}\): Ao avaliarmos o valor p-value para a estatística t referente ao \(\beta_{2}\) da regressão (coeficiente relacionado à variável independente “airplay”), observamos que p-value < 0,05, indicanddo que o \(\beta_{2}\) deve fazer parte do modelo final de regressão. Além disso, o valor de \(\beta_{2}\) é 3,59. Isso indica que, para cada aumento de 1 unidade nas quantidade de vezes que o álbum é tocado nas rádios, espera-se que ocorra um aumento de 3,59 unidades vendidas do álbum. Por exemplo, se tivermos 100 novas vezes na qual o álbum for tocado nas rádios, espera-se uma elevação de 359 unidades vendidas desse álbum.
4.3 Akaike Information Criteria (AIC)
Além da métrica do R-squared, podemos também usar a métrica Akaike Information Criteria (AIC) como medida alterantiva para a avaliar o desempenho dos modelos de regressão linear. Usamos também o AIC, pois o grande problema do R-squared é que quando você adiciona mais variáveis ao modelo, ele vai aumentar. Dessa forma, ele sensível ao aumento de variáveis independentes no modelo. Assim, se você está decidindo qual dos dois modelos se ajusta melhor aos dados, o modelo com mais as variáveis preditoras se ajustarão melhor, pois o R-squared será maior. Para solucionar isso, podemos usar medidas de ajustes que penalizam a inclusão de mais variáveis independentes no modelo. É isso que faz o AIC. Com isso, prioriza-se o modelo mais parcimonioso. No código abaixo, estimamos o AIC para os dois modelos estimados até aqui: advertSalesModel e advertAirplaySalesModel.
# Calcular o AIC para o modelo aicAdvertSalesModel
aicAdvertSalesModel <- AIC(
object = advertSalesModel
)
aicAdvertSalesModel## [1] 2247.375# Calcular o AIC para o modelo aicAdvertAirplaySalesModel
aicAdvertAirplaySalesModel <- AIC(
object = advertAirplaySalesModel
)
aicAdvertAirplaySalesModel## [1] 2132.398A análise do AIC se dá sempre de forma comparativa. Comparando-se os valores de AIC entre dois ou mais modelos. Aquele modelo com menor valor de AIC será o modelo com melhor ajuste aos dados. Ao análisarmos os valores de AIC para os modelos testados, verificamos que o valor de AIC do modelo advertSalesModel (com uma variável independente) é 2247.37 e do modelo advertAirplaySalesModel (com duas variáveis independentes) é 2132.40. Diante disso, já levando em conta a penalização por incluir uma variável a mais no modelo advertAirplaySalesModel, esse modelo possui uma AIC menor e é, portanto, o modelo com melhor ajuste.
4.4 Checagem das suposições do modelo de regressão linear
4.4.1 Independência entre os resíduos (erros)
Para quaisquer duas observações, os termos residuais (erros) devem ser não correlacionados (ou independentes). Essa eventualidade é descrita como falta de autocorrelação. Para testar a falta de autocorrelação entre os resíduos utiliza-se o teste de Durbin–Watson. Nesse teste, a hipótese nula é de ausência de autocorrelação entre os resíduos. Portanto, esperamos não rejeitar a hipótese nula (p-value > 0,05).
## lag Autocorrelation D-W Statistic p-value
## 1 -0.05150748 2.055283 0.656
## Alternative hypothesis: rho != 0O valor do p-value para a estatística durbin watson é 0.684 (p-value > 0,05). Portanto, aceita-se a hipótese nula de que os resíduos não são autocorrelacionados.
4.4.2 Multicolinearidade
A multicolinearidade existe quando há uma forte correlação entre dois ou mais preditores em um modelo de regressão. A multicolinearidade representa um problema apenas para a regressão múltipla, porque, por óbvio, a regressão simples possui apenas uma variável preditora. Se houver colinearidade perfeita entre os preditores, torna-se impossível obter estimativas únicas dos coeficientes de regressão porque há um número infinito de combinações de coeficientes que funcionariam igualmente bem. Se tivermos dois preditores perfeitamente correlacionados, então os valores de \(\beta\) para cada variável são intercambiáveis. Ou seja, não temos confiabilidade para a estimação dos betas.
Há algumas medidas que podem ser usadas para checar se há ou não multicolinearidade entre os preditores. A medida base para esses teste é o fator de inflação de variância (variance inflation factor - VIF). O VIF indica se um preditor tem uma forte relação linear com o(s) outro(s) preditor(es). Embora não existam regras rígidas e rápidas sobre qual valor do VIF deve causar preocupação, temos três avaliações a ser realizadas:
Se o maior VIF for maior que 10, então há motivo para preocupação (Bowerman & O’Connell, 1990; Mayers, 1990).
Relacionada ao VIF está a estatística de tolerância, que é seu recíproco (1/VIF). Assim, valores para a estatística de tolerância abaixo de 0,1 indicam sérios problemas, embora Menard (1995) sugere que valores abaixo 0,2 já são dignos de preocupação.
Se o VIF médio for substancialmente maior que 1, a regressão pode ser tendenciosa (Bowerman & O’Connell, 1990).
## adverts airplay
## 1.010489 1.010489Nenhum valor de VIF sendo maior que 10, então não há motivo para preocupação com multicolinearidade.
## adverts airplay
## 0.9896199 0.9896199Nenhum valor para a estatística de tolerância está abaixo de 0,2, então não há motivo para preocupação com multicolinearidade.
## [1] 1.010489Valor médio de VIF não é substancialmente maior do que 1, então não há motivo para preocupação com multicolinearidade.
4.4.3 Suposições sobre linearidade, homocedasticidade dos resíduos e erros normalmente distribuídos
Linearidade: Os valores médios da variável de resultado para cada incremento do o(s) preditor(es) está(ão) ao longo de uma linha reta. Em inglês simples, isso significa que é assumido que a relação que estamos modelando é linear. Se modelarmos uma relação não linear usando um modelo linear, isso obviamente limita a generalização das descobertas
Homocedasticidade: Em cada nível da(s) variável(is) preditora(s), a variância dos termos residuais deve ser constante. Isso significa apenas que os resíduos em cada nível do(s) preditor(es) deve(m) ter a mesma variância (homocedasticidade). Quando as variações são muito desiguais, diz-se que há heterocedasticidade.
Erros normalmente distribuídos: assume-se que os resíduos no modelo são aleatórios, variáveis normalmente distribuídas com média 0. Essa suposição significa simplesmente que as diferenças entre o modelo e os dados observados são mais frequentemente zero ou muito próximas de zero, e que diferenças muito maiores que zero acontecem apenas ocasionalmente. Algumas pessoas confundem essa suposição com a ideia de que os preditores devem ser distribuído normalmente. Os preditores não precisam ser normalmente distribuídos.
Para checar essas três suposições, podemos plotar o gráfico dos resíduos versus os valores preditores pelo modelo (fitted). De acordo com (Field, Miles, and Field 2012), o quadrante indicado como “normal” na figura abaixo é o resultado que indica o atendimento dessas três suposições.
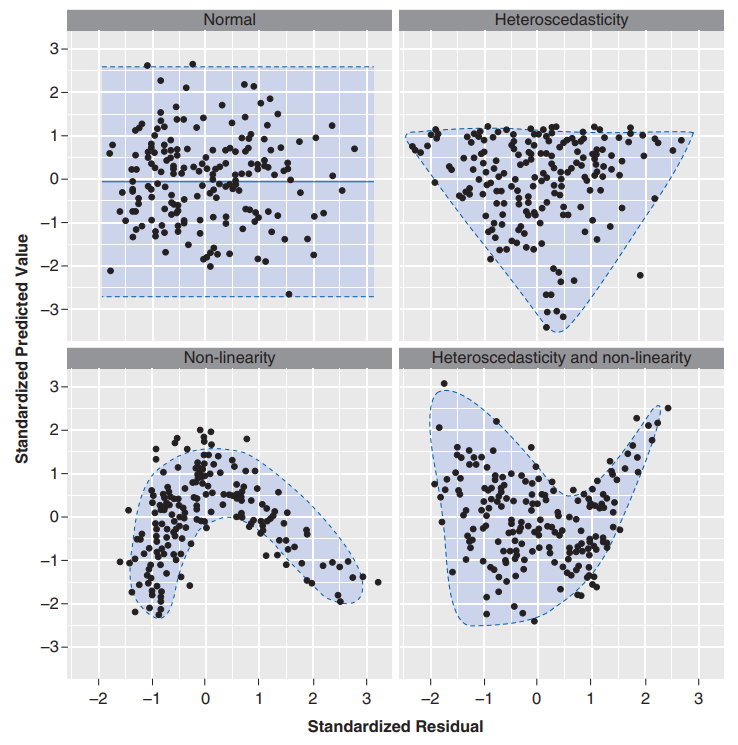
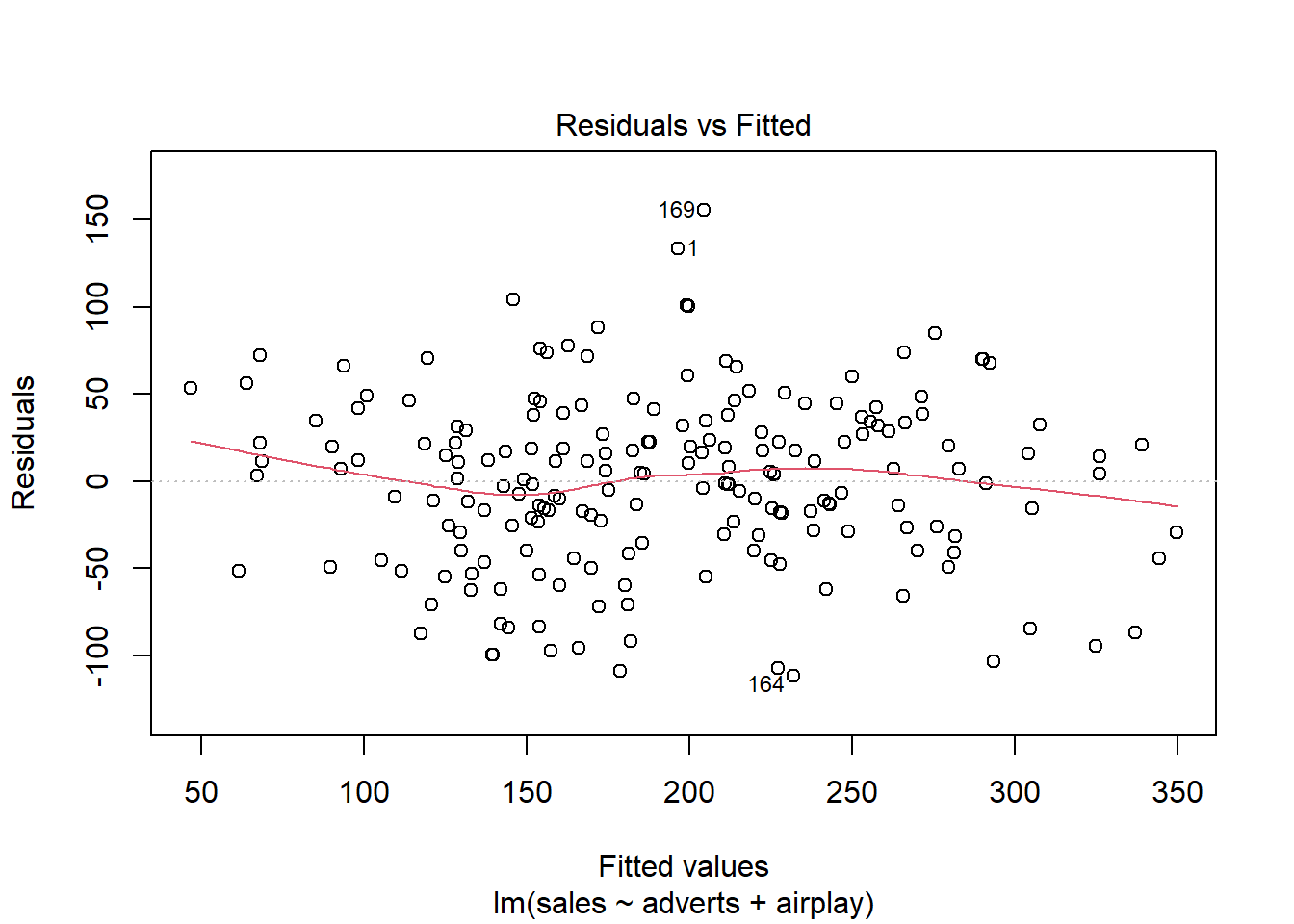
O gráfico acima está mais próximo do cenário normal.
Além disso, sobre checar se os resíduos (erros) seguem uma distribuição normal, podemos também plotar o histograma dos resíduos, o QQ plot e fazer o teste de Shapiro-Wilk.
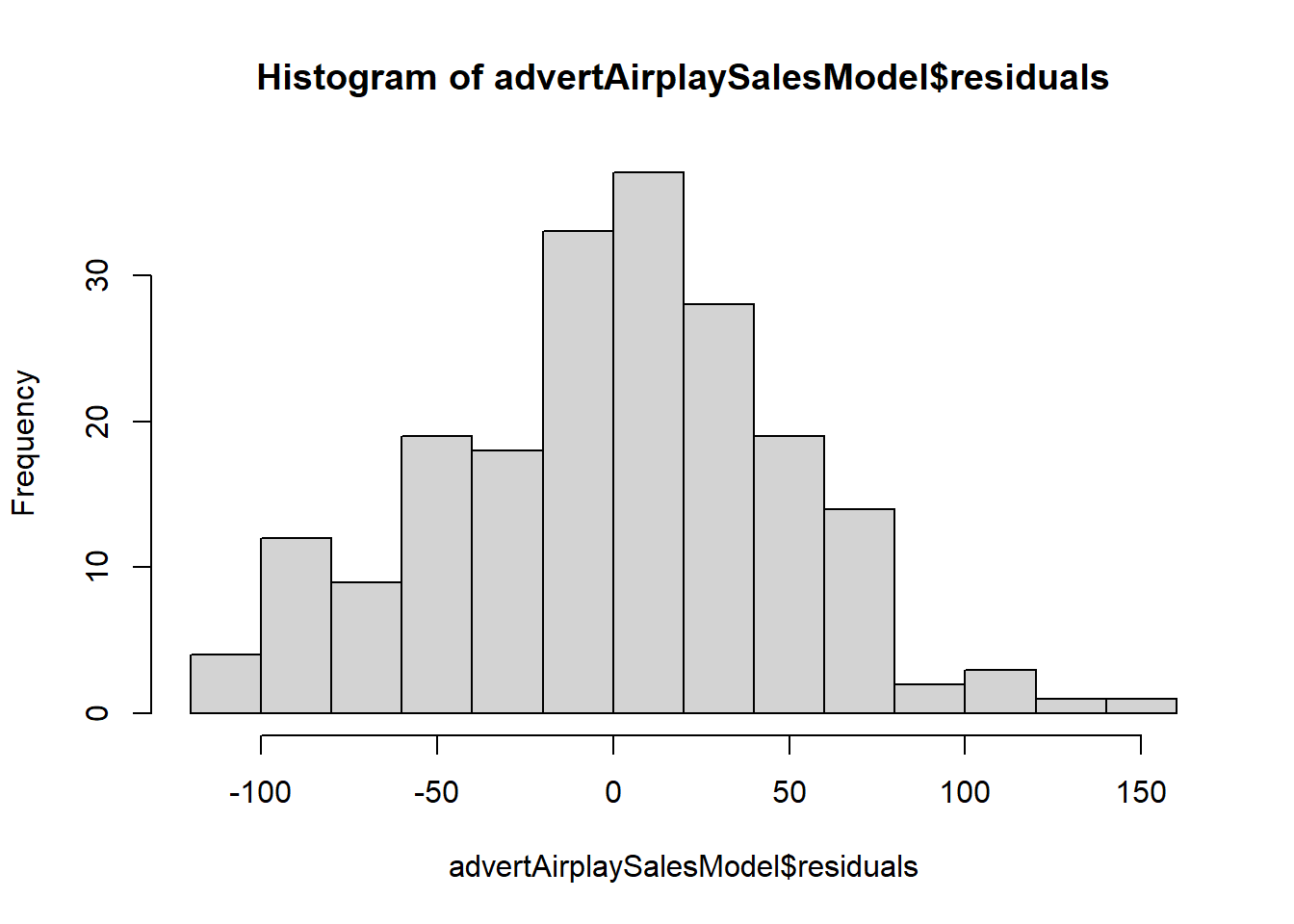
Aqui, no histograma dos resíduos, temos uma comportamento compatível com uma distribuição normal.
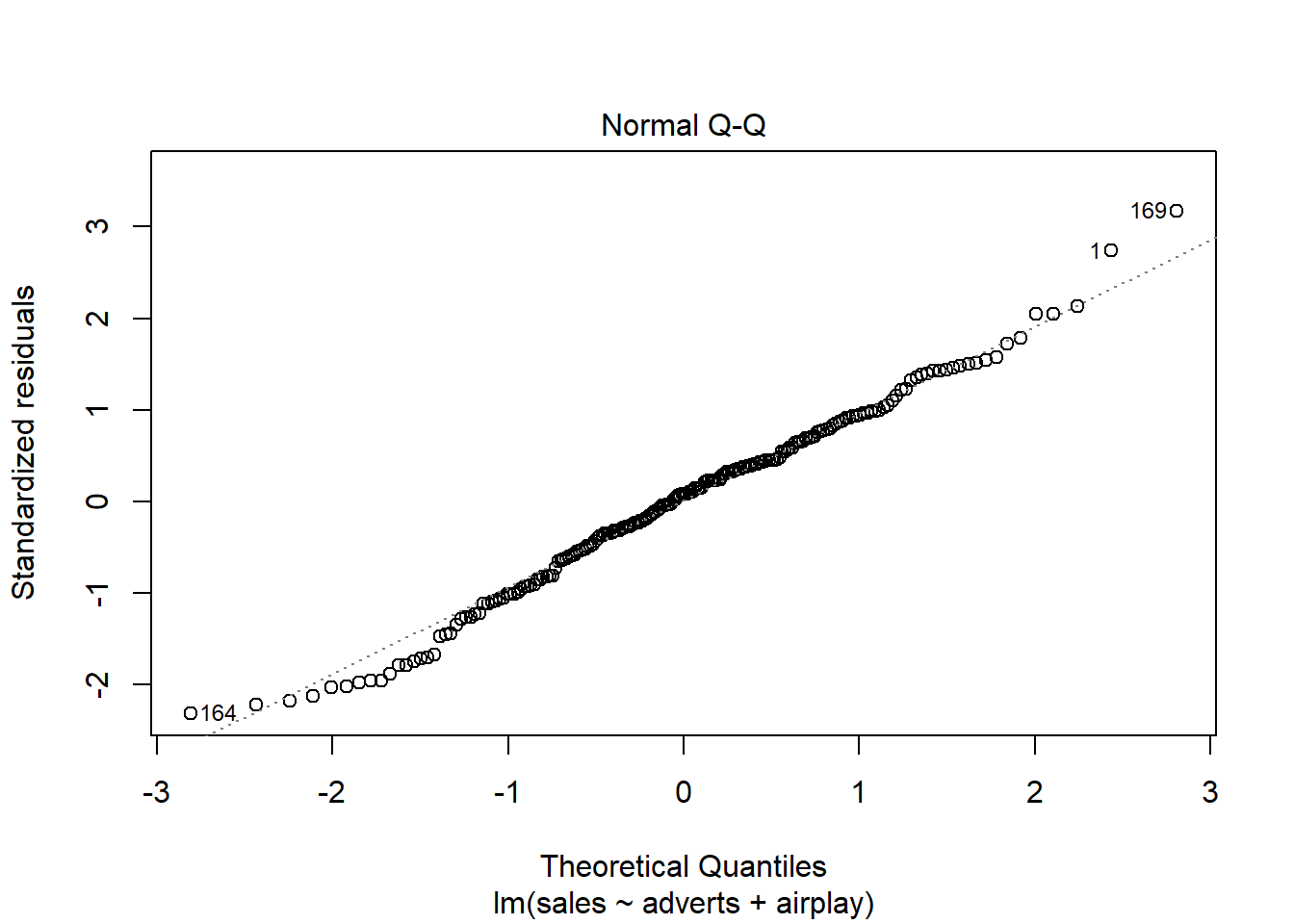
O resultado do QQ plot deve apresentar os resíduos próximos da linha diagonal do gráfico. Nesse caso, podemos afimar que isso está ocorrendo, compatível com uma distribuição normal.
Por fim, a distribuição normal dos resíduos pode ainda ser chacada utilizando o teste de Shapiro-Wilk. No teste de Shapiro-Wilk, a hipótese nula é que os dados seguem a distribuição normal.
# Fazer o teste Shapiro-Wilk para testar se os resíduos são nomalmente distribuídos
shapiro.test(advertAirplaySalesModel$residuals)##
## Shapiro-Wilk normality test
##
## data: advertAirplaySalesModel$residuals
## W = 0.9913, p-value = 0.2741Como o p-value > 0,05, então aceitamos a hipótese nula que os resíduos seguem a distribuição normal.
4.5 Predição utilizando o modelo de regressão estimado
Todo modelo de regressão estimado, formado por seus parâmetros, pode ser utilizado para estimar o valor da variável dependente dados valores específicos para as variáveis independentes. Para isso, basta ter uma base de dados com os valores para as variáveis independentes do modelo de regressão estimado (com os nomes das colunas iguais aos nomes )
# Criar uma base de casos novos de álbuns para os quais queremos prever as
# quantidades vendidas.
baseTeste <- data.frame(
adverts = c(105.65, 1504.25, 554.98),
airplay = c(85, 47, 2)
)
baseTeste## adverts airplay
## 1 105.65 85
## 2 1504.25 47
## 3 554.98 2Nessa base de teste criada, temos três novos casos de álbuns para os quais queremos projetar as unidades vendidas. Para fazer essa predição, podemos usar a função predict() conforme o código abaixo.
# Usar o modelo advertAirplaySalesModel para predizer
qtdVendasPreditas <- predict(
object = advertAirplaySalesModel,
newdata = baseTeste
)
qtdVendasPreditas## 1 2 3
## 355.35054 340.49679 96.52197Ao aplicar o modelo advertAirplaySalesModel para os três casos novos, temos as quantidades projetadas acima para cada um desses álbuns. Abaixo, apresenta-se manualmente como foi feita predição para que você tenha a intuição de como realizar a predição via modelo de regressão linear.
# solicitar o summary do modelo advertAirplaySalesModel para verificar os valores dos parâmetros
summary(advertAirplaySalesModel)##
## Call:
## lm(formula = sales ~ adverts + airplay, data = albumSales)
##
## Residuals:
## Min 1Q Median 3Q Max
## -112.121 -30.027 3.952 32.072 155.498
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 41.123811 9.330952 4.407 1.72e-05 ***
## adverts 0.086887 0.007246 11.991 < 2e-16 ***
## airplay 3.588789 0.286807 12.513 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 49.38 on 197 degrees of freedom
## Multiple R-squared: 0.6293, Adjusted R-squared: 0.6255
## F-statistic: 167.2 on 2 and 197 DF, p-value: < 2.2e-16Agora usa-se os parâmetros para fazer cada predição. Compare cada valor com o resultado da função predict() rodada acima para apenas comprovar que os valores feitos manualmente ou via a função predict() são os mesmos.
# Predição manual para os três casos
beta0 <- advertAirplaySalesModel$coefficients[1]
beta1 <- advertAirplaySalesModel$coefficients[2]
beta2 <- advertAirplaySalesModel$coefficients[3]
predCaso1 <- beta0 + beta1 * 105.65 + beta2 * 85
predCaso2 <- beta0 + beta1 * 1504.25 + beta2 * 47
predCaso3 <- beta0 + beta1 * 554.98 + beta2 * 2
conferencia <- bind_cols(
PredFuncaoPredict = qtdVendasPreditas,
PredManual = c(predCaso1, predCaso2, predCaso3)
)
conferencia## # A tibble: 3 × 2
## PredFuncaoPredict PredManual
## <dbl> <dbl>
## 1 355. 355.
## 2 340. 340.
## 3 96.5 96.5