Capítulo 2 Análise Descritiva de Dados
Em uma análise descritiva de dados, busca-se explorar os dados e utilizar métodos de estatística descritiva para entender o padrão dos dados observados. A partir de medidas como média, mediana, desvio padrão e análise das distribuições de frequência das variáveis analisadas, o cientista de dados toma conhecimento inicial sobre os dados, chega a insights preliminares e identifca as possibilidades de aprofundamento das análises.
2.1 Tipos de variáveis
Variáveis são apenas fenômenos observados que variam (Renda, escolaridade, margem de lucro, etc.). Uma variável que entendemos ser uma causa ou ser útil para prever outra variável, chamamos de variável independente (porque seu valor não depende de outra variável) ou de variável preditiva. Ao passo que aquela variável que entendemos ser um efeito ou uma resposta esperada, chamamos de variável dependente (porque depende de uma causa) ou variável resposta (Field, Miles, and Field 2012).
2.2 Níveis de medição de variáveis
A relação entre o que está sendo medido e os números que representa o que está sendo medido é conhecido como o nível de medição (Field, Miles, and Field 2012). Diante disso, em um nível mais geral, as variáveis podem ser categóricas ou contínuas.
2.2.1 Variáveis categóricas
As variáveis categóricas são aquelas nas quais os valores são categorias. Elas podem ser:
- Variáveis binárias: Variáveis compostas por apenas dois valores categóricos que não possuem nenhuma ordem implícita entre as categorias.
Exemplo 2.1 (Status do cliente): Cliente ativo ou cliente inativo.
Exemplo 2.2 (Status de chuva): Está chovendo ou não está chovendo.
- Variáveis nominais: Variáveis compostas por mais do que dois valores categóricos que não possuem nenhuma ordem implícita entre as categorias.
Exemplo 2.3 (Espécies de cães): labrador, bulldog, poodle, etc.
- Variáveis ordinais: Variáveis compostas por valores categóricos que possuem ordem implícita entre as categorias.
Exemplo 2.4 (Escolaridade): ensino fundamental, ensino médio, curso técnico, graduação, mestrado e doutorado
2.2.2 Variáveis contínuas
As variáveis contínuas são aquelas que nos dão uma pontuação para cada entidade e podem assumir qualquer valor na escala de medida que estamos usando. Elas podem ser:
- Variáveis intervalares: Variáveis formadas por escalas convencionadas nas quais temos a certeza de que intervalos iguais na escala representam diferenças iguais na propriedade que está sendo medida.
Exemplo 2.5 (Escalas Likert): uma escala do tipo Likert, que vai do valor 1 até valor 5. Essa é uma variável intervalar, pois a diferença entre as avaliações de utilidade de 1 e 2 é convencionado que será a mesma que a diferença entre, digamos, 3 e 4, ou 4 e 5. Da mesma forma, a diferença na utilidade entre as classificações de 1 e 3 é idêntica à diferença entre as notas de 3 e 5.
Exemplo 2.6 (Escalas Celsius): Na escala Celsius, para medição de temperatura, os valores dessa escala foram convencionados entre a temperatura de congelamento e de ebulição da água, de forma que o 0 graus Celsius não significa ausência completa de temperatura. No entanto, intervalos iguais na escala Celsius representam diferenças iguais da temperatura medida.
- Variáveis de razão: Variáveis nas quais, além atenderem aos requisitos de uma variável de intervalar, a escala deve ter um valor zero que seja verdadeiro.
Exemplo 2.7 (Escala Kelvin): Diferentemente da escala Celsius, que é uma variável intervalar, a escala Kelvin, para medição de temperatura, é uma variável de razão, pois o ponto de 0 graus Kelvin significa efetivamente o ponto de ausência de temperatura.
2.3 Validade e confiabilidade
Imagine que precisamos desenvolver um instrumento para mensurar o peso das pessoas. Nosso desejo é que esse instrumento tenha um baixo erro de medição da variável peso. Uma maneira de tentar garantir que o erro de medição seja mínimo é determinar propriedades da medida que nos deem confiança de que ela está fazendo seu trabalho corretamente.
Validade: A primeira propriedade é a validade, que indica se um instrumento realmente mede o que se propõe a medir.
Confiabilidade: A segunda propriedade é a confiabilidade, que indica se um instrumento pode ser interpretado consistentemente em diferentes situações.
Em relação à validade, precisamos garantir que o instrumento utilizado realmente seja capaz de medir a variável peso. Em um exercício hipotético, se o cientista escolher um termômetro para medir peso, estará utilizando uma medida não válida para medir peso. O correto é utilizar uma balança, capaz de efetivamente medir peso.
Em relação à confiabilidade, precisamos garantir que o instrumento utilizado realmente seja capaz de apresentar consistemente o mesmo resultado em diferente ocasiões de medição. Em um exercício hipotético, se o cientista escolher uma balança para medir peso, podemos dizer que esse instruimento é confiável se, por exemplo, dada uma pessoa que pesa 80kg, o instrumento apresenta resultados bastante próximos do peso real (80kg) com consistência, após realizadas diferentes pesagens dessa pessoa.
2.4 Realizando análises descritivas de dados
2.4.1 Distribuição de frequência
Depois de coletar alguns dados, uma coisa muito útil a fazer é traçar um gráfico de quantas vezes cada valor ocorre. Isso é conhecido como distribuição de frequência, ou histograma, que é um gráfico que traça valores de observações no eixo horizontal, com uma barra mostrando quantos vezes cada valor é observado no conjunto de dados (eixo vertical). As distribuições de frequência podem ser muito úteis para avaliar propriedades da distribuição dos valores observados para uma dada variável.
Para realizar as análises descritivas, utilizaremos a base de dados sobre os ratings de facebook, disponibilizada por (Field, Miles, and Field 2012) no repositório de dados desse ebook.
Essa base de dado se refere a um estudo sobre os ratings de fotos de perfil de usuários do facebook (avaliadas em termos de coolness, fashion, attractiveness and glamour), que tenta prever o quanto as pessoas que postaram as fotos pontuam em uma escala de narcisismo. Na base de dados há as seguintes variáveis:
- id: um número indicando o código identificador do usuário que postou a foto.
- NPQC_R_Total: o escore total para o instrumento utilizado para medir narcisismo.
- Rating_Type: indica se o rating apresentado na variável “Rating” se refere à coolness, glamour, fashion ou attractiveness.
- Rating: o escore de rating dado para a foto avaliada (em uma escala likert de 1 a 5).
O código permite criar um histograma para a variável NPQC_R_Total e outro para a variável Rating.
# Carrega o pacote tidyverse para usar funções de manipulação dos variáveis
library(tidyverse)
# Carregar base de dados facebookData.csv do livro de Field et al. (2012)
facebookData <- read.csv(
# No parâmetro file, use o caminho para a pasta onde está
# o arquivo facebookData.csv em seu computador.
file = "dados/facebookData.csv",
header = TRUE
)
# Criar o histograma da variável NPQC_R_Total
facebookData %>%
select(NPQC_R_Total) %>%
pull() %>%
hist(main = "Histograma - NPQC_R_Total")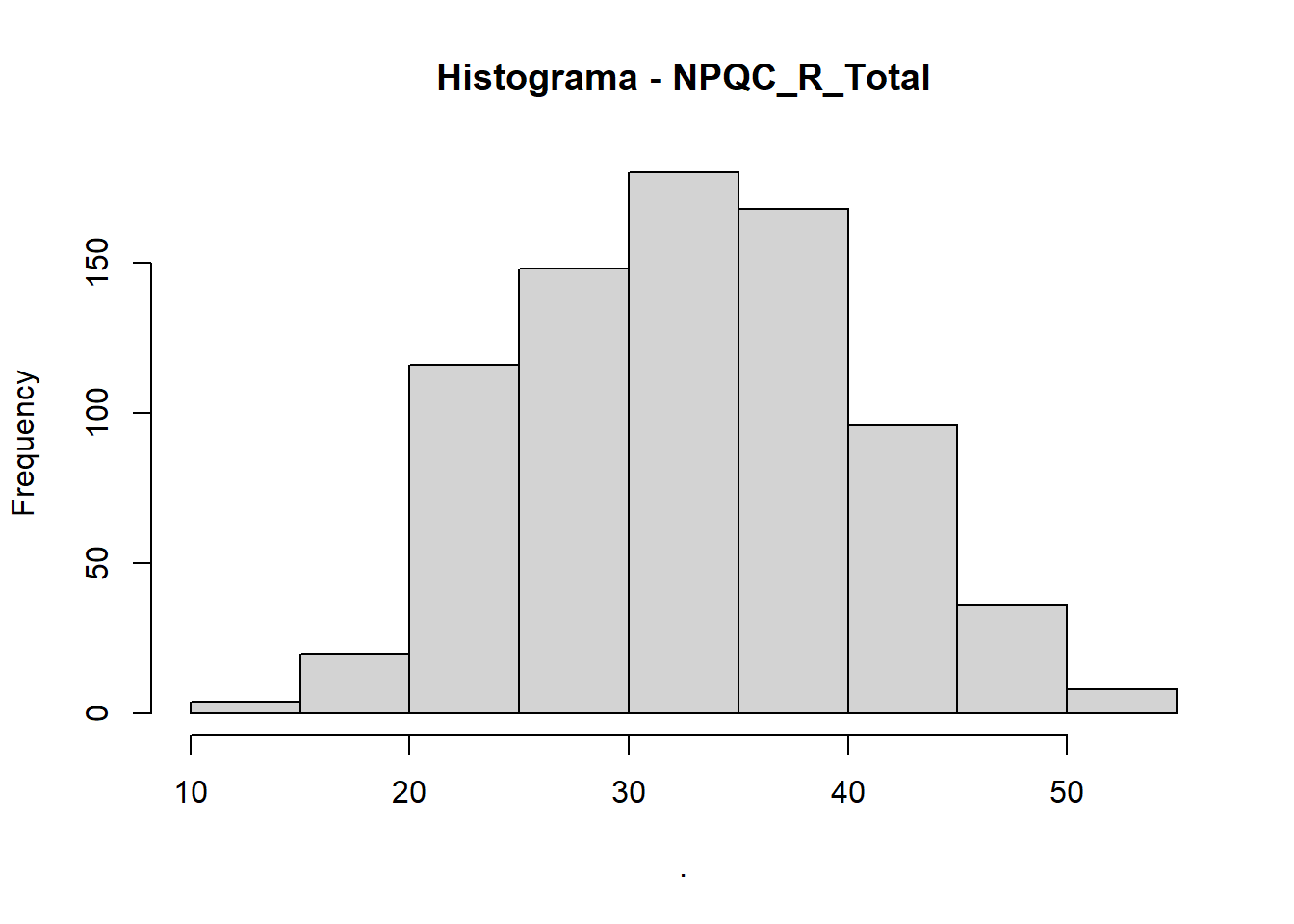
# Criar o histograma da variável Rating
facebookData %>%
select(Rating) %>%
pull() %>%
hist(main = "Histograma - NPQC_R_Total")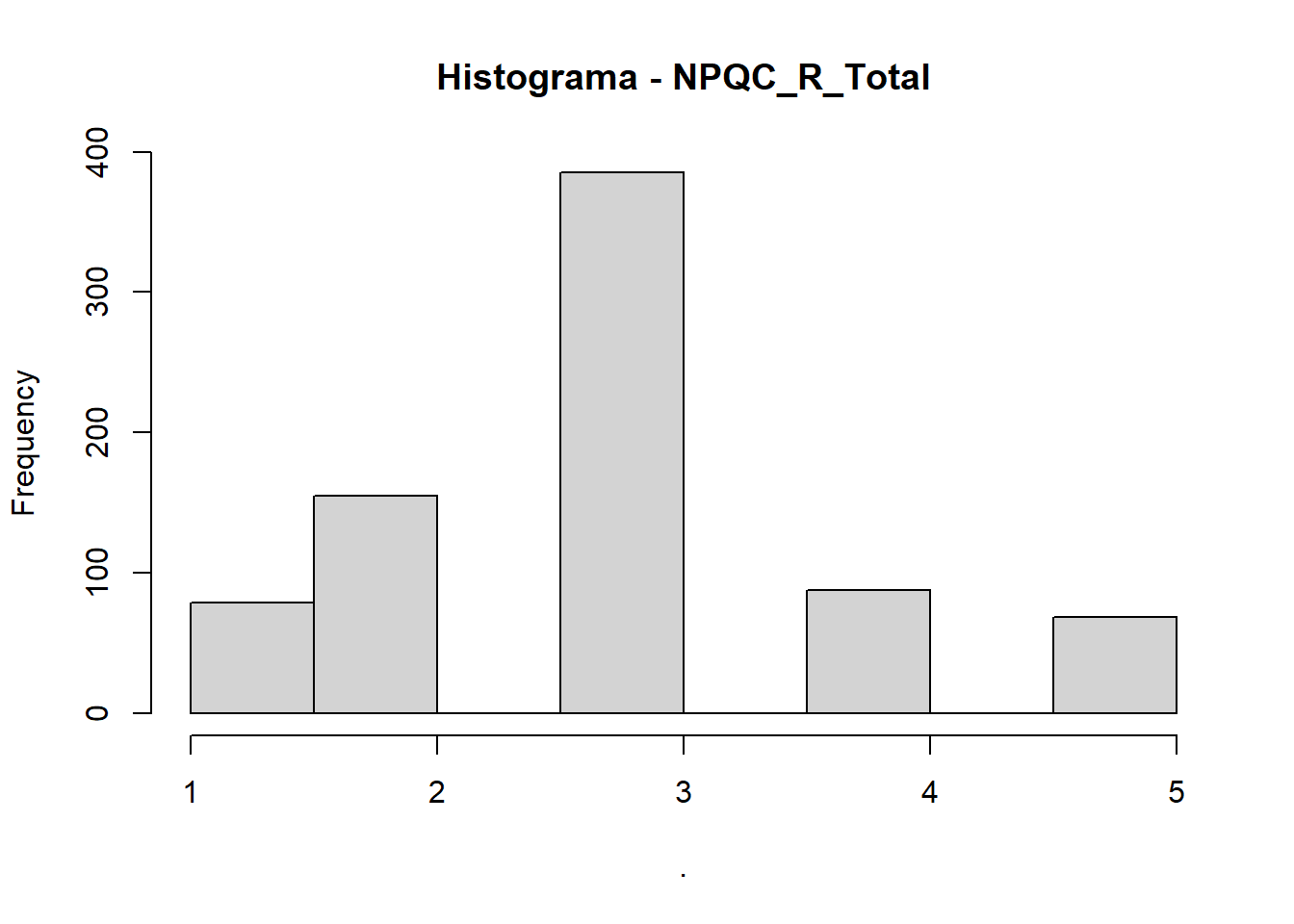
2.4.2 Média
A média é a medida de tendência central da qual você provavelmente já ouviu falar porque na TV e nas mídias sociais vemos médias apresentadas por todos os lados. Para calcular a média, nós simplesmente somamos todas os valores da distribuição e depois dividimos pela quantidade total de valores. O cálculo da média no R é feito utilizando a função “mean()”. No código abaixo, calcula-se a média da variável NPQC_R_Total.
# Calcular a média da variável NPQC_R_Total
facebookData %>%
summarise(
NPQC_R_Total_Media = mean(NPQC_R_Total)
)## NPQC_R_Total_Media
## 1 33.163562.4.3 Moda
A moda é simplesmente o valor que ocorre com mais frequência no conjunto de dados. Isso é fácil de detectar em uma distribuição de frequência, porque será a barra mais alta! O cálculo da moda no R é feito utilizando a função “Mode()” (precisa carregar o pacote “pracma” para usar essa função). No código abaixo, calcula-se a moda da variável NPQC_R_Total.
# Carregar o pacote "pracma" para poder usar a função "Mode()"
library(pracma)
# Calcular a moda da variável NPQC_R_Total
facebookData %>%
summarise(
NPQC_R_Total_Moda = Mode(NPQC_R_Total)
)## NPQC_R_Total_Moda
## 1 362.4.4 Quantis
Quantis são medidas que dividem um conjunto de dados ordenados (do menor ao maior valor) em k partes iguais.
2.4.4.1 Mediana
A mediana é o valor que está na posição que divide exatamente ao meio uma distribuição de valores ordenada do menor valor ao maior. Portanto, na mediana k = 2, uma vez que a mediana divide a distribuição de valores em duas partes. No código abaixo, calcula-se a mediana da variável NPQC_R_Total de duas maneiras alternativas:
(\(i\)) Utilizando a função “median()”, que é o método tradicional.
(\(ii\)) Utilizando a função “quantile()” para retonar exatamente o percentil 50%.
Perceba que ambos os caminhos levam ao mesmo valor de resultado.
# Calcular a mediana da variável NPQC_R_Total
facebookData %>%
summarise(
NPQC_R_Total_Median1 = median(NPQC_R_Total),
NPQC_R_Total_Median2 = quantile(
x = NPQC_R_Total,
probs = 0.5
)
)## NPQC_R_Total_Median1 NPQC_R_Total_Median2
## 1 33 332.4.4.2 Outros quantis frequentemente utilizados
Além da mediana que divide uma distribuição exatamente ao meio. Temos também outras opções frequentemente utilizadas para dividir uma distribuição de valores.
- Quartis: dividem a distribuição em quatro partes (k = 4) de tamanhos iguais. Para isso, há três quartis: Q1 = 25%; Q2 = 50%; Q3 = 75%. O cálculo dos quartis é feito utilizado a função “quantile()”. No código abaixo, calcula-se os quartis da variável NPQC_R_Total:
# Calcular os quartis da variável NPQC_R_Total
facebookData %>%
summarise(
Quartis = c(0.25, 0.5, 0.75),
NPQC_R_Total_Quartis = quantile(
x = NPQC_R_Total,
probs = c(0.25, 0.5, 0.75)
)
)## Quartis NPQC_R_Total_Quartis
## 1 0.25 27.44
## 2 0.50 33.00
## 3 0.75 38.00- Decis: dividem a distribuição em dez partes (k = 10) de tamanhos iguais. Para isso, há 9 decis: D1 = 10%; D2 = 20%; D3 = 30%; D4 = 40%; D5 = 50%; D6 = 60%; D7 = 70%; D8 = 80%; D9 = 90%. O cálculo dos decis é feito utilizado a função “quantile()”. No código abaixo, calcula-se os decis da variável NPQC_R_Total:
# Calcular os decis da variável NPQC_R_Total
facebookData %>%
summarise(
Decis = c(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9),
NPQC_R_Total_Decis = quantile(
x = NPQC_R_Total,
probs = c(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9)
)
)## Decis NPQC_R_Total_Decis
## 1 0.1 23
## 2 0.2 26
## 3 0.3 29
## 4 0.4 31
## 5 0.5 33
## 6 0.6 35
## 7 0.7 37
## 8 0.8 40
## 9 0.9 44- Percentis: dividem a distribuição em 100 partes (k = 100) de tamanhos iguais. Para isso, há 99 percentis: P1 = 1%; P2 = 2%; P3 = 3% […] P97 = 97%; P98 = 98%; P99 = 99%. O cálculo dos percentis é feito utilizando-se a função “quantile()”. No código abaixo, calcula-se os percentis da variável NPQC_R_Total:
# Calcular os percentis da variável NPQC_R_Total
facebookData %>%
summarise(
Percentis = seq(
from = 0.01,
to = 0.99,
by = 0.01
),
NPQC_R_Total_Percentis = quantile(
x = NPQC_R_Total,
probs = seq(
from = 0.01,
to = 0.99,
by = 0.01
)
)
)## Percentis NPQC_R_Total_Percentis
## 1 0.01 18.50
## 2 0.02 19.00
## 3 0.03 20.25
## 4 0.04 21.00
## 5 0.05 22.00
## 6 0.06 22.00
## 7 0.07 22.00
## 8 0.08 23.00
## 9 0.09 23.00
## 10 0.10 23.00
## 11 0.11 23.00
## 12 0.12 23.47
## 13 0.13 24.00
## 14 0.14 24.00
## 15 0.15 25.00
## 16 0.16 25.00
## 17 0.17 25.00
## 18 0.18 25.50
## 19 0.19 26.00
## 20 0.20 26.00
## 21 0.21 26.00
## 22 0.22 26.00
## 23 0.23 27.00
## 24 0.24 27.00
## 25 0.25 27.44
## 26 0.26 28.00
## 27 0.27 28.00
## 28 0.28 28.00
## 29 0.29 29.00
## 30 0.30 29.00
## 31 0.31 29.00
## 32 0.32 30.00
## 33 0.33 30.00
## 34 0.34 30.00
## 35 0.35 30.00
## 36 0.36 30.00
## 37 0.37 30.00
## 38 0.38 31.00
## 39 0.39 31.00
## 40 0.40 31.00
## 41 0.41 31.00
## 42 0.42 31.00
## 43 0.43 31.06
## 44 0.44 32.00
## 45 0.45 32.00
## 46 0.46 32.00
## 47 0.47 33.00
## 48 0.48 33.00
## 49 0.49 33.00
## 50 0.50 33.00
## 51 0.51 33.00
## 52 0.52 34.00
## 53 0.53 34.00
## 54 0.54 34.00
## 55 0.55 34.00
## 56 0.56 35.00
## 57 0.57 35.00
## 58 0.58 35.00
## 59 0.59 35.00
## 60 0.60 35.00
## 61 0.61 36.00
## 62 0.62 36.00
## 63 0.63 36.00
## 64 0.64 36.00
## 65 0.65 36.00
## 66 0.66 36.00
## 67 0.67 36.00
## 68 0.68 36.00
## 69 0.69 37.00
## 70 0.70 37.00
## 71 0.71 37.00
## 72 0.72 37.06
## 73 0.73 38.00
## 74 0.74 38.00
## 75 0.75 38.00
## 76 0.76 38.00
## 77 0.77 38.00
## 78 0.78 39.00
## 79 0.79 39.00
## 80 0.80 40.00
## 81 0.81 40.00
## 82 0.82 40.26
## 83 0.83 41.00
## 84 0.84 41.00
## 85 0.85 41.00
## 86 0.86 41.00
## 87 0.87 42.00
## 88 0.88 42.00
## 89 0.89 42.00
## 90 0.90 44.00
## 91 0.91 44.00
## 92 0.92 45.00
## 93 0.93 45.00
## 94 0.94 45.00
## 95 0.95 47.00
## 96 0.96 48.00
## 97 0.97 48.75
## 98 0.98 50.00
## 99 0.99 50.252.4.5 Máximo e mínimo
O cálculo dos valores de máximo e mínimo representam o maior valor observado e o menor valor observado em uma distribuição respectivamente. No código abaixo, calcula-se os valores máximo e mínimo da variável NPQC_R_Total:
# Calcular o máximo e o mínimo da variável NPQC_R_Total
facebookData %>%
summarise(
NPQC_R_Total_Min = min(NPQC_R_Total),
NPQC_R_Total_Max = max(NPQC_R_Total)
)## NPQC_R_Total_Min NPQC_R_Total_Max
## 1 14 522.4.6 Variância
A variância é uma medida que avalia o grau de dispersão dos valores de uma distribuição em torno da média. A variância indica o quanto, em média, os dados variam ao quadrado em torno da média. O cálculo da variânica é feito utilizando-se a função “var()”. No código abaixo, calcula-se a variância da variável NPQC_R_Total:
# Calcular a variância da variável NPQC_R_Total
facebookData %>%
summarise(
NPQC_R_Total_Variancia = var(NPQC_R_Total)
)## NPQC_R_Total_Variancia
## 1 58.015992.4.7 Desvio padrão
O desvio padrão é outra uma medida que avalia o grau de dispersão dos valores de uma distribuição em torno da média. O desvio padrão é igual a raiz quadrada da variância. Ele geralmente é mais utilizado do que a variância para a apresentação de análises de dispersão de distribuições de valores, pois o valor do desvio padrão possui a mesma unidade de medida que a da variável analisada. O desvio padrão, portanto, indica o quanto, em média, os dados variam em torno da média. O cálculo dos percentis é feito utilizando-se a função “sd()”. No código abaixo, calcula-se o desvio padrão da variável NPQC_R_Total:
# Calcular o desvio padrão da variável NPQC_R_Total
facebookData %>%
summarise(
NPQC_R_Total_Desvio_Padrao = sd(NPQC_R_Total)
)## NPQC_R_Total_Desvio_Padrao
## 1 7.616823Quando os dados seguem uma distribuição normal, podemos utilizar propriedades interessantes da medida de desvio padrão conforme apresentado na figura abaixo.
Entre o intervalo [\(média - DP; média + DP\)], compreendemos 68,26% dos valores.
Entre o intervalo [\(média - 2*DP; média + 2*DP\)], compreendemos 95,44% dos valores.
Entre o intervalo [\(média - 3*DP; média + 3*DP\)], compreendemos 99,72% dos valores.

Além do entendimento do conceito de desvio padrão, é importante também conhecer o efeito da variação do valor do desvio padrão na distribuição de uma variável. Para simularmos esse efeito, no código abaixo geraremos duas variáveis, \(x_{1}\) e \(x_{2}\), criadas a partir de duas gerações aleatórias de distribuições normais com médias \(m_{1}\) e \(m_{2}\), bem como desvios padrão \(dp_{1}\) e \(dp_{2}\). Na simulação feita, com o objetivo de observar o efeito do desvio padrão na distribuição das duas variáveis criadas, as médias das duas distribuições serão as mesmas, \(m_{1} = m_{2} = 10\). Ao passo que os desvios padrão serão diferentes, \(dp_{1} = 1\) e \(dp_{2} = 4\).
# Criar as duas variáveis geradas de distribuições normais
x1 <- rnorm(
n = 100000, # distribuição com 100000 observações
mean = 10, # média = 10
sd = 1 # desvio padrão = 1
)
x2 <- rnorm(
n = 100000, # distribuição com 100000 observações
mean = 10, # média = 10
sd = 4 # desvio padrão = 4
)
# Plotar os histogramas para as variáveis x1 e x2
hist(
x = x1,
xlim = c(-10,30)
)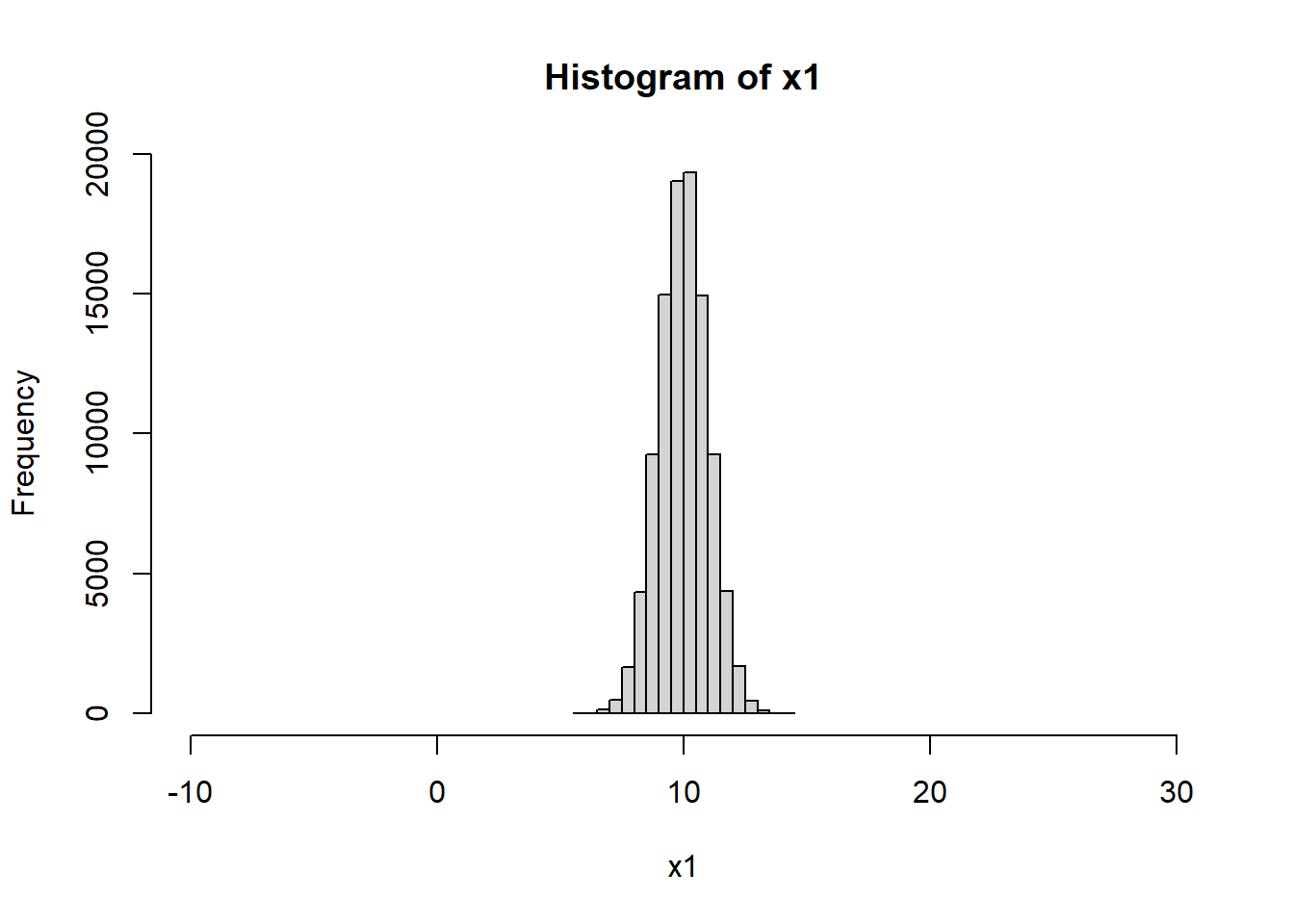
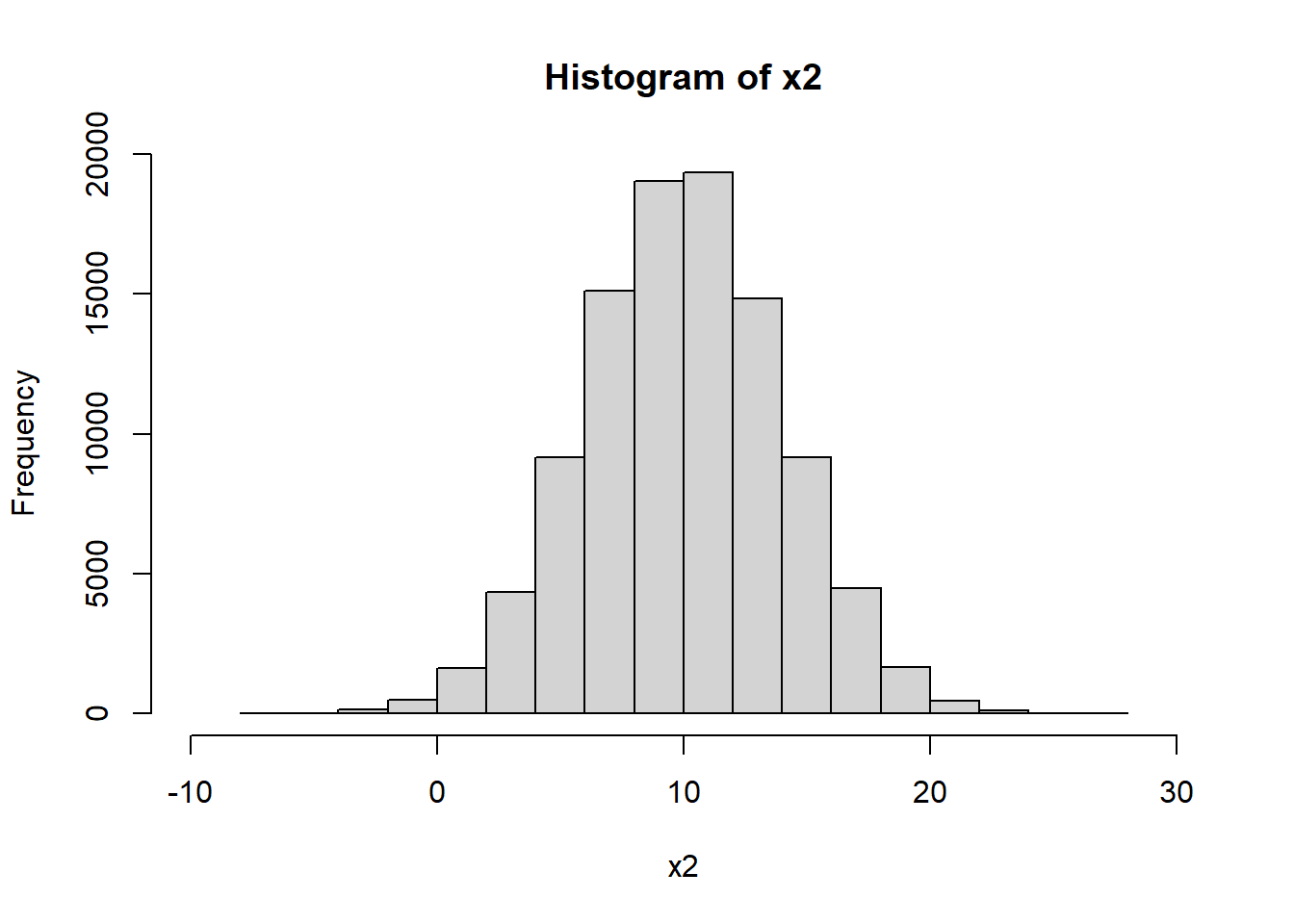
Observe que, embora as médias das distribuições de \(x{1}\) e \(x_{2}\) sejam as mesmas, a dispersão dos valores em torno da média é maior em \(x_{2}\) quando comparado com \(x_{1}\). Isso implica que quanto maior for o valor do desvio padrão, maior será a dispersão dos valores em torno da média.
2.4.8 Resumo de variáveis descritivas com pacote skimr
Até vimos separadamente o cálculo das medidas de estatística descritiva, compreendendo significado de cada uma delas. Agora que sabemos como analisar essas medidas, podemos usar o software para calcular todos elas de uma só vez e ainda para diversas variáveis ao mesmo tempo, economizando assim tempo no processo de análise descritiva de dados. Para fazer isso, podemos usar a função “skim()” do pacote skimr.
# Carregar o pacote skimr para poder usar as medidas de estatística descritiva
library(skimr)
# Calcular as medidas de estatística descritiva
facebookData %>%
select(
NPQC_R_Total,
Rating
) %>%
skim()| Name | Piped data |
| Number of rows | 776 |
| Number of columns | 2 |
| _______________________ | |
| Column type frequency: | |
| numeric | 2 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| NPQC_R_Total | 0 | 1 | 33.16 | 7.62 | 14 | 27.44 | 33 | 38 | 52 | ▁▆▇▅▂ |
| Rating | 0 | 1 | 2.89 | 1.03 | 1 | 2.00 | 3 | 3 | 5 | ▂▃▇▂▂ |
Os resultados acima mostram os resultados de diversas medidas descritivas para as duas variáveis que queremos analisar (NPQC_R_Total e Rating). As seguintes medidas são calculadas para cada variável:
n_missing: calcula a quantidade de observações faltantes (missings)
complete_rate: calcula a razão entre a quantidade de observações não faltantes sobre o total de observações da variável analisada. No extremo superior, esse valor será 1 se não houver nenhuma observação faltante e, no outro extremo inferior, será 0 se todas as observações estiverem faltantes.
mean: calcula a média
sd: calcula o desvio padrao
p0: calcula o percentil 0
p25: calcula o percentil 25, que é também o primeiro quartil
p50: calcula o percentil 50, que é também a mediana e o segundo quartil
p75: calcula o percentil 75, que é também o terceiro quartil
p100: calcula o percentil 100
hist: apresenta uma versão miniatura do histograma dessa variável
2.4.9 Erro padrão (Standard Error)
O erro padrão também é uma medida de variabilidade. No entanto, é diferente do desvio padrão, que avalia o grau de dispersão dos valores de uma distribuição em torno da média, ficando restrito aos valores dentro da amostra disponível. O erro padrão é uma medida inferencial, que mede o grau de incerteza em torno da estimativa da medição da média, ou seja, mede a precisão de média calculada a partir de nossa amostra. O erro padrão, portanto, indica o quão bem os dados de nossa amostra representam toda a população. Essa medida é bastante utilizada para o cálculo de um intervalo de confiança em torno de nossa estimativa de média amostral (Altman and Bland 2005).
No código abaixo, calcula-se o erro padrão para a variável NPQC_R_Total:
# Calcular o erro padrão da variável NPQC_R_Total
facebookData %>%
summarise(
NPQC_R_Total_Erro_Padrao = sd(NPQC_R_Total) / sqrt(length(NPQC_R_Total))
)## NPQC_R_Total_Erro_Padrao
## 1 0.2734282.4.10 Intervalo de confiança em torno da média
A partir do conhecimento do valor do erro padrão, é possível calcular o intervalo de confiança em torno da média estimada em nossa amostra. Para isso, no entanto, precisamos primeiro definir o nível de confiança desejada para nossa estimativa do intervalo de confiança e encontrar o valor critico do Z-score correspondente a esse nível de confiança. Para entender como definir o Z-score, assista a essa tutorial do Khan Academy: Como encontrar o valor do Z-score utilizando a Tabela Z. Em ciências sociais, é comum utilizarmos o intervalo de confiança de \(95\%\), para o qual o Z-score correspondente é \(1,96\). Tendo-se o valor do erro padrão e do Z-score, é possível calcular o intervalo de confiança para a média amostral da seguinte forma:
\[ \text{Limite superior do IC} = \overline{X} + (Z_{\frac{1-p}{2}} * SE) \] \[ \text{Limite inferior do IC} = \overline{X} - (Z_{\frac{1-p}{2}} * SE) \]
No código abaixo, calcula-se o intervalo de confiança para a média da variável NPQC_R_Total:
# Calcular o intervalo de confiança da variável NPQC_R_Total
zScore95Perc <- 1.96 # Z-acore para nível de confiança de 95%
facebookData %>%
summarise(
NPQC_R_Total_Media = mean(NPQC_R_Total),
NPQC_R_Total_Desvio_Padrao = sd(NPQC_R_Total),
NPQC_R_Total_Erro_Padrao = NPQC_R_Total_Desvio_Padrao / sqrt(length(NPQC_R_Total)),
NPQC_R_Total_Media_Limite_Superior = NPQC_R_Total_Media + (zScore95Perc * NPQC_R_Total_Erro_Padrao),
NPQC_R_Total_Media_Limite_Inferior = NPQC_R_Total_Media - (zScore95Perc * NPQC_R_Total_Erro_Padrao)
) %>%
t()## [,1]
## NPQC_R_Total_Media 33.163557
## NPQC_R_Total_Desvio_Padrao 7.616823
## NPQC_R_Total_Erro_Padrao 0.273428
## NPQC_R_Total_Media_Limite_Superior 33.699476
## NPQC_R_Total_Media_Limite_Inferior 32.627638Assim, diante dos valores de NPQC_R_Total_Media, NPQC_R_Total_Media_Limite_Superior e NPQC_R_Total_Media_Limite_Inferior, a média amostral da variável NPQC_R_Total é 33,16 com intervalo de confiança de \(95\%\) igual a [32,63; 33,70].